Flexion simple
Définition : Flexion
Une poutre est soumise à la flexion lorsque les forces qui lui sont appliquées tendent à faire varier sa courbure.
La flexion est dite simple, lorsque la poutre possède un plan de symétrie et que les forces fléchissantes agissent dans ce plan, perpendiculairement au grand axe de la poutre.
Efforts tranchants, moments fléchissants
Si on imagine une coupure en un point
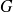qui divise la poutre en deux parties notées
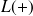et
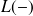. Chacune de ces deux parties est en équilibre sous l'action des efforts extérieurs qu'elle reçoit et sous l'action en
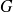de l'autre partie.équilibre global de la poutre :
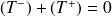
équilibre de la partie
:
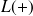L'effort tranchant
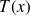dans une section d'abscisse
, séparant la poutre orientée en une parie
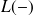et une partie
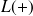, est la résultante des forces extérieures s'exerçant sur
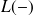.Le diagramme des efforts tranchants est la courbe représentative de la fonction
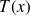en fonction de
.
Le moment fléchissant
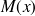dans une section d'abscisse
, séparant la poutre orientée en une partie
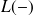et une partie
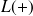, est la somme des moments extérieurs (dus aux couples concentrés et aux efforts d'action et de réaction) s'exerçant sur
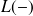.Le diagramme des moments fléchissants est la courbe représentative de la fonction M(x) en fonction de
.
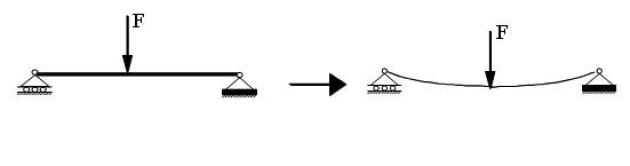
Déformée d'une poutre soumise à la flexion simple : flèche
Sous l'effet des sollicitations auxquelles elle est soumise, une poutre se déforme.
On désigne par flèche à l'abscisse
, le déplacement du centre de gravité de la section correspondant à cette abscisse.
Elle est comptée positivement si le déplacement s'effectue vers le haut. Le nouveau lieu des centres de gravité de toutes les sections de la poutre prend le nom de déformée.
On admet la relation suivante qui permet le calcul de la déformée :
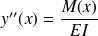avec
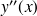est la dérivée seconde de la flèche par rapport à
,-
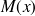, le moment fléchissant à la section d'abscisse
,
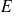, le module d'élasticité longitudinale (module d'Young),
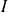, le moment d'inertie de la section par rapport à l'axe
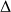passant par le centre de gravité et perpendiculaire au plan moyen de la poutre.
