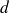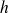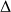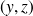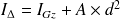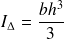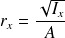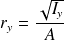Éco-construction d'un bâtiment à énergie positive

Cours
Outils

Formule de Huyggens

Fondamental : Formule de Huygens (translation d'axes)

Soit une surface d'aire 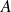et de centre de gravité (coordonnées dans le repère .

L'axe horizontal et l'axe vertical 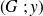passent par le centre de gravité de la surface .

On cherche les moments quadratiques et 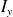par rapport aux axes 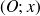et situés aux distances 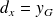et de l'axe horizontal et l'axe vertical .

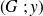On a :

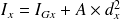
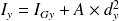
Exemple :

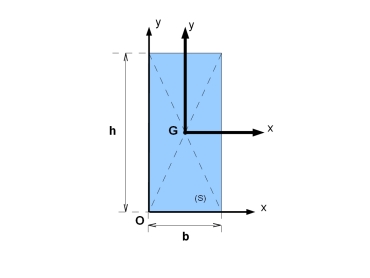
Représentation dans le plan d'un rectangle homogène plein. Le centre d'inertie G du cercle a pour coordonnées horizontale (abscisse) x=b/2 et verticale (ordonnée) y=h/2.

Rectangle de largeur b et de hauteur h

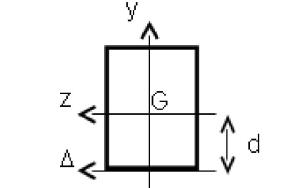
Dans le cas d'un déplacement du moment vers l'axe situé sur la base du rectangle, étant la distance entre le centre de gravité 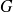, centre du repère 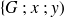et la base du rectangle ( ) :

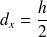Finalement on trouve .

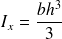Exemple : Autres notations.

Rectangle de largeur b et de hauteur h.

Rectangle (matériau homogène) de largeur , de longueur et d'aire .

Dans le cas d'un déplacement du moment vers l'axe situé sur la base du rectangle, étant la distance entre , centre du repère et la base du rectangle ( ) :

Application :

Rayon de giration

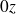Le rayon de giration noté relatif à l'axe d'une surface plane d'aire 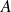s'exprime en :

En particulier on a :

Accueil

Imprimer Co-auteurs : Yves Ardourel, Estelle Bretagne, Jean-Michel Decuq, Smail Khainnar, Patrizia Laudati, Manuel Mesquita, Martine Rey, Michel Reznikoff / Coordinatrice pédagogique : Estelle Bretagne / Production : UVED - Université de lorraine, production audiovisuelle et multimédia, Direction du Numérique.