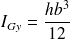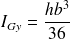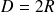Éco-construction d'un bâtiment à énergie positive

Cours
Outils

Moment quadratique ou moment d'inertie

Définition : Moment quadratique ou d'inertie

Les moments quadratiques ou d'inertie d'une surface par rapport à l'axe horizontal (0 ;x) et à l'axe verticale (0 ;y) sont :

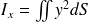
(unités : m⁴)

Attention : Formulaires

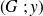Dans les formulaires, les moments quadratiques sont donnés le plus souvent par rapport aux axes et où 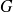est le centre de gravité de la surface . Dans ce cas nous écrirons les moments quadratiques et 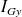pour éviter toute confusion.

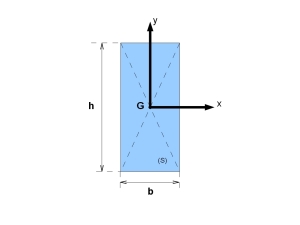
Représentation dans le plan d'un rectangle homogène plein de centre d'inertie G. Cette fois le centre du repère est choisi au centre d'inertie, c'est-à-dire en G. Les coordonnées du point G sont donc (0 ;0) dans ce repère.

Rectangle de largeur b et de hauteur h

Cas du rectangle (matériau homogène) ; attention le centre du repère est pris en G centre d'inertie du rectangle :

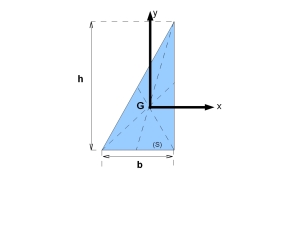
Représentation dans le plan d'un triangle homogène plein de centre d'inertie G. Cette fois le centre du repère est choisi au centre d'inertie, c'est-à-dire en G. Les coordonnées du point G sont donc (0 ;0) dans ce repère.

Triangle rectangle de base b et de hauteur h

Cas du triangle rectangle de base b et de hauteur h (matériau homogène) ; attention le centre du repère est pris en G centre d'inertie du triangle rectangle :

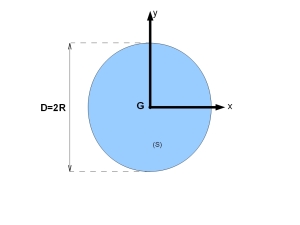
Représentation dans le plan d'un disque homogène plein de rayon R et de centre d'inertie G. Cette fois le centre du repère est choisit au centre d'inertie, c'est-à-dire en G. Les coordonnées du point G sont donc (0 ;0) dans ce repère.

Disque de rayon R et de centre G.

Cas d'un disque de diamètre (matériau homogène) ; attention le centre du repère est pris en G centre d'inertie du disque :

Exemple : Trapèze perforé (exemple de figures composées)

Décomposition d'un trapèze plein mais perforé en la somme de plusieurs figures : un rectangle plein, un triangle plein et la soustraction d'un disque plein.

Exemple à 2 dimensions d'un trapèze perforé.

On a les propriétés suivantes :

Accueil

Imprimer Co-auteurs : Yves Ardourel, Estelle Bretagne, Jean-Michel Decuq, Smail Khainnar, Patrizia Laudati, Manuel Mesquita, Martine Rey, Michel Reznikoff / Coordinatrice pédagogique : Estelle Bretagne / Production : UVED - Université de lorraine, production audiovisuelle et multimédia, Direction du Numérique.