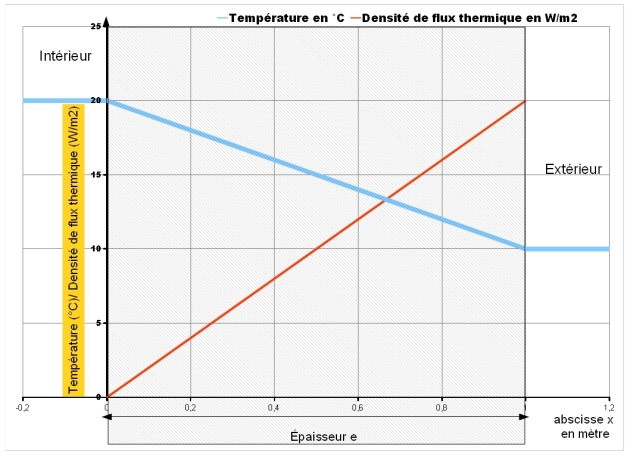
Conduction dans une paroi d'épaisseur e
Complément : Conduction dans une paroi d'épaisseur e
On considère un mur plan dont les dimensions latérales sont très supérieures à son épaisseur
 (effets de bord négligeables) et soumis sur ses faces à des conditions aux limites uniformes.
(effets de bord négligeables) et soumis sur ses faces à des conditions aux limites uniformes.
Soit
 la direction orthogonale au mur (dans l'épaisseur). Avec les hypothèses énoncées ci-dessus, on suppose que la température ne dépend que de l'abscisse
la direction orthogonale au mur (dans l'épaisseur). Avec les hypothèses énoncées ci-dessus, on suppose que la température ne dépend que de l'abscisse
 et que le problème est monodimensionnel ou 1D.
et que le problème est monodimensionnel ou 1D.
On définit les grandeurs ci-dessous :
la densité de flux d'énergie thermique :
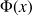 (W/m2) (Pertes caloriques),
(W/m2) (Pertes caloriques),la conductivité thermique :
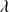 (W/°C.m),
(W/°C.m),le champ de température fonction de l'abscisse notée
 :
:
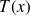 (en °C).
(en °C).
La grandeur
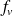 désigne le débit de production ou de perte exprimé en W.m-3 ; c'est l'énergie produite au sein même du matériau d'épaisseur
désigne le débit de production ou de perte exprimé en W.m-3 ; c'est l'énergie produite au sein même du matériau d'épaisseur
 . Cette grandeur est souvent nulle, mais il y a des cas où elle ne l'est pas. Ici on suppose que
. Cette grandeur est souvent nulle, mais il y a des cas où elle ne l'est pas. Ici on suppose que
 .
.
On suppose que le transfert d'énergie sous forme de chaleur s'effectue seulement par conduction.
Objectifs :
Calculer la température en tout point de la paroi (
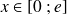
En déduire les valeurs de flux pour déterminer les pertes.
Conditions aux limites (CL) :
Température intérieure imposée en
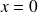 :
:

Température extérieure en
 :
:
 ;
;
Épaisseur
 ;
; Coefficient de conductivité
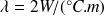 .
.
Loi de Fourier :
 .
.
Équilibre thermique régi par :
 , ce qui donne ici :
, ce qui donne ici :
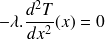
On déduit que
 et
et
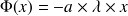 où
où
 et
et
 sont deux nombres constants à déterminer.
sont deux nombres constants à déterminer.
A l'aide des conditions aux limites, on en déduit que :
 ,
, .
.
Fondamental : Conduction dans une paroi d'épaisseur e
La température varie linéairement dans l'épaisseur de la paroi.
On trouve que la densité de flux d'énergie thermique
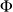 est proportionnelle à :
est proportionnelle à :
la conductance U,
l'écart de température.
Plus la conductance est grande, plus la densité de flux de chaleur à travers la paroi est grande.
Inversement la résistance thermique va représenter « l'aptitude de la paroi à s'opposer au passage de la chaleur »
(d'après l'
ouvrage de Christian Lemaître[1]).